A. The space of rays and transformations in it.

We consider a system of lenses, each (initially) with a center lying along a common central ray C which passes through the lenses unchanged. The basic items of analysis are the rays of light passing through these lenses. A ray is determined by a direction and a point along it, which in 2 space would be 3 parameters, except that all points along a given ray r determine the same r, so the space of rays in 2D is 2-dimensional. Similarly in 3-space the space of rays is 4-dimensional, and in n-space is 2(n -1)-dimensional.

For the 2D situation we wish to analyze first, rays r near the central ray C can be parametrized by their distance y from C and their angle t to it. (Angles pointing up from C count as positive.) If r is inclined to C we must state where along C the distance from C will be measured. Two points along each segment of c, its first and last, are natural for this purpose.

Rays r passing through our system are transformed in two ways: by incidence and by distance. At incidence to the front surface or exit from the back surface of one of our lenses, the angle (but not the position) of a ray changes. Since our rays travel in straight lines, distance changes the position but not the angle of a ray r, always in the same simple way. If r is at distance y from a segment s of C of length d at its start, and at angle t, then r is at distance y + d sin(t) at the end of s.

The change of angle at an incidence is governed by Snell's' law:

sin(refracted_angle) = c * sin(angle_of_incidence),

where c is the optical density (refractive index) of the medium being left divided by that of the medium being entered, and angles are measured from the incoming normal to the ray. At an air-to-glass or air-to-oil transition this is typically 1/1.5. At air-to-water it is 1/1.33. Thus rays entering a denser medium are bent toward the incoming normal, and rays entering a less-dense medium are bent away from it. Particularly dense glass, e.g. 70% lead flint glass and Arsenic Trisulfide glass have higher refractive indices: 1.8 and 2.0 respectively. The refractive index is color-dependent in a manner determined by the materials involved, generally dropping as we go from blue to red. For example, for dense flint it goes from 1.8 (blue) to 1.7 (red), while for borosilicate crown it goes from 1.3 (blue) to 1.1 (red).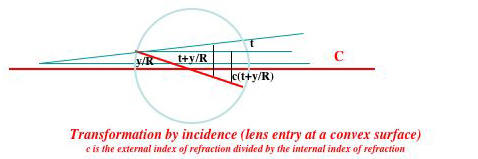

Near its center line the surface of a lens is well enough approximated by a circle of radius R. Thus if a ray r is at distance y and angle t from the center line C at the point at which C enters a lens L, its angle of incidence is t + arcsin (y)/R, and so after refraction its angle to the incoming normal will be c(t + arcsin(y)/R) and its angle to the horizontal C will be c(t + arcsin (y)/R) - arcsin (y)/R = ct + (c - 1) arcsin(y)/R. For small y this is well enough approximated by ct + (c - 1)y/R, and the distance transformations above by the formula y + dt. So (inevitably) for rays r near C, i.e. for small y and t, these transformations are (inevitably) linear, and have matrices

|1 d|  (distance transformation)     and |1          0| (incidence transformation). 
|0 1|                                    |(c - 1)/R  c|

Since this and our following formulas neglect higher order terms, they can be said to represent the 'first order' ray theory of lenses.

This basic approximation is valid only for rays passing near a lens's center. So the discussion which follows ignores all those concerns of commercial lens designers having to do with the behavior of a lens's whole surface. These are vital issues in the design of wide-angle and fish-eye lenses, and also in precise elimination of various kinds of whole-lens focusing faults such as spherical aberration. Our treatment of these more advanced issues will be sketchy.

Whenever a series of lens surfaces occur one after another separated by distances d_1,d_2, ... the preceding formulas apply. A common case is that of a single lens of thickness d with two convex surfaces of radii r1 and r2. At the exiting surface its angle of incidence is t - arcsin (y)/R so after refraction its angle to the outgoing normal will be (t + arcsin(y)/R)/c and its angle to the horizontal C will be (t - arcsin (y)/R)/c + arcsin (y)/R = t/c + (1 - 1/c) arcsin(y)/R. For small y this is well enough approximated by t/c + (1 - 1/c)y/R. The matrix of this transformation is

|1          	0| (incidence transformation at exit from a convex lens surface). 
|(1 - 1/c)/R  1/c|

The preceding discussion has assumed that the lens surfaces encountered are convex. But if some of them are concave, the same formulas apply except that for a concave surface the entering geometry is the same as that of the exiting transition for a convex lens and the exiting geometry is the same as that of the entering transition for a convex lens. Therefore the transition matrices for these two transformations are

|1          0| (incidence transformation at entry to a concave lens surface). 
|(1 - c)/R  c|

and

|1          	0| (incidence transformation at exit from a concave lens surface). 
|(1/c - 1)/R  1/c|

B. Focus. Consider the family of rays emanating at various angles from a point p near C, whose distance from the point q at which C enters the first lens in a sequence is d and whose distance from C is y. In our line coordinates at q these have the form [y + dt,t]. Conversely, consider any family of rays near C which have the form [at + b,a't + b'] at the point at which they exit the last lens in a sequence. First suppose that a and a' have opposite signs, a being positive and 'a' negative. Then if these rays propagate to a point q' a distance -a/a' further along C, their coordinates at that point will be [b - ab'/a',a't + b']. That is, all of these points pass thru a common point at distance b - ab'/a' from the center ray C. This fact, which tells us that rays originating a a common point before entering a ray system always converge to a common point after exiting the system, is associated with the term 'Focus'. at the focus the rays are turned the amount b' from their original angles, and initial deviations from the horizontal are multiplied by the common factor a'.

Suppose the initial focus p moves by an amount z in a direction perpendicular to the center ray C. Then rays emanating from p at various angles will have the form [y + z + dt,t], and so at their exit from the final lens of our sequence they will have the form [at + b + mz,a't + b'+ m'z]. If we let them propagate the same distance -a/a' further along C as in the preceding paragraph, they will take on the form [b - ab'/a' + mz,a't + b'+ m'z], i.e will all pass thru the point b - ab'/a' + mz above the center ray C at point q' along it. Thus if the initial focus p moves by an amount z in a direction perpendicular to the center ray C, the final focus q moves by the amount mz in the same direction. So light emanating in various directions from the points along a line L perpendicular to C come to focus along another line perpendicular to C. The same fact holds for lenses in 3D that are circularly symmetric about a center ray C, but with 'line' becoming 'plane'. That is, light emanating in various directions from the points along a plane L perpendicular to C come to focus along another plane perpendicular to C. It is this fact that gives rise to the term 'focal plane'.

To determine how the positions of the initial and final focus planes relate, we can start with rays emanating from a point q on the central ray at distance d from its entry into the first lens. In coordinates at this entry point, these have the form [dt,t], so on exit from the last lens they will have the form [(ad + b)t,(a'd + b')t],

Finding the focus and testing whether a set of rays comes to a focus. If the family of rays emanating from a point eventually come to focus, the intersection of any two of the rays in it determines the position of the focus. Conversely if a relatively few of a randomly chosen subset of the rays E emanating from a point all pass through some other common point p, then since the situation with which we deal is described by simple algebraic equations it is highly likely that all of the other rays in E pass through p, which must therefore be the focus of the family E of rays. This probabalistic approach can also be used to determine whether a family of rays comes to an approximate rather than an exact focus, i.e. if there is a point p such that all the rays in E pass within distance r of p. For this, begin by tracing any two rays of E, and find the closest distance of approach of these rays and the two points p₁ and p₂ at which this closest approach is realized. Estimate the approximate focus p of the whole family E as the point halfway between p₁ and p₂. Then if there is any point q such that all the rays in E pass within distance r of q, p must lie within distance r from q, so all the other rays in E must pass within distance 2r of p. This can be tested by selecting, e.g. 10 rays of E at random, and seeing if any fail to pass this close to p. If not then it is highly unlikely that 10% of the rays in E fail to pass within distance 2r of p, since in this case the observation just made has probability 10^-10.

Virtual (and real) images. If in the above discussion a and a' do not have opposite signs, so that -a/a' is negative, then if they could be propagated backwards they would converge to a focus q_v. Even though this is impossible, the group of rays appear as if they came at various angles from the point q_v. Also, just as in the case considered above, motion of the initial focus of a family of rays in a direction perpendicular to the central ray C moves the point of virtual focus in a direction perpendicular to C. So virtual images, like real images, lie along virtual lines of focus (or, in 3-dimensions, virtual planes of focus.)

Lens focal lengths and the lens transformation matrix. The focal length of a lens is the distance beyond the lens (or, for concave lenses, before the lens) at which a parallel beam of rays coming from infinity (such a group of rays is said to be 'collimated') will come to focus. There are actually two focal lengths, one for rays entering the lens from the left, the other from the right, which need not be the same except for symmetrical lenses.

If the incidence transformation of the first and second lens surfaces are

|1 0|   and    |1  0|
|a 1|          |a' 1|

respectively, and if the lens thickness is d, the lens's transformation matrix is

|1 + a'd             d|
|a + a' + aa'd  1 + ad|     

[(D(1 + da') + d)t,(D(a + a' + aa'd)) + (1 + ad))t].

Thus they come to focus after a distance

(D(1 + a'd) + d)/(D(a + a' + aa'd)) + (1 + ad)).

This can be written as

(D(1 + a'd)/(D(a + a' + aa'd))) + d/(D(a + a' + aa'd)))/ (1 + (1 + ad)/(D(a + a' + aa'd))).

which is

(Df_i + d/(D(a + a' + aa'd)))/ (1 + f_o).

so if we define k = d/(a + a' + aa'd), rays originating at distance D before the lens come to focus at distance (Df_i + k/D)/ (1 + f_o) after it. The value k can be called the 'supplementary focus parameter' of the lens.

This lets us describe the action any lens in terms of the three focal-plane related parameters [f_o,f_i,k]. In terms of these three parameters, the plane of focus of rays originating a distance D in front of the lens is . it is also easy to find the algebraic expressions for the lens transformation parameters [a,a',d] in terms of these three parameters, since

Focus of partially blocked lenses. Suppose that the surface of a lens is partially blocked, for example by a circular grid of narrow opaque stripes of width substantially larger than the wavelength of the light passing through the lens to the sensor behind it, e.g a stripe separation of 1 millimeter or more. Then rays encountering one of these stripes will simply be deleted. But the surviving rays will come to focus in the same way as for an unblocked lens, and so the geometry of focus remains unchanged except that the intensity of the focused image is reduced. I.e. blocking of a lens by a totally opaque grid on or very near it has a minimal effect on the focus image formed, be this real or virtual. Note that the effect of such a grid is far less than that of a few translucent smears on the lens surface, such as might be caused by touching the lens surface. This is because such a smear scatters light unpredictably into the rest of the image, causing it to blur rather than to diminish cleanly in intensity.

Measuring the focal plane transformation function of a commercial lens system. In order to use a high-quality commercial lens L in combination with external lenses or with some other commercial lens, one needs to know its focal plane transformation function. The problem is that L will often consist of many internal optical elements, i.e. sub-lenses and even mirrors, perhaps fifteen or more. As L's focus is adjusted, some of these elements move. Still more, if L is a zoom lens with a separate zoom adjustment, other internal motions take place as the zoom ring is manipulated. In this thicket of complications there is only one thing one can count on: when properly focused on an object at distance D from the camera, the camera forms a focused real image on its sensor, which is always at a known fixed distance of a few centimeters from L's inside end. But this gives us only one value of L's focal plane transformation function aD + B/a'D + b': two more are needed.

To make the measurements needed for this, one wants to know how (without refocusing) L treats objects at two other, significantly different, distances D and D'. This can be measured by detaching L form the camera which normally carries it, and using a second camera to measure the position of the focused real image of object at these distances which L will form. For measurement convenience, this second camera should be one with macro capability and a good digital zoom, able to focus anywhere from 3 to 25 centimeters in front of its lens. Before being used, this second camera should be calibrated, i.e the setting of its focusing ring should be associated with the distance to the object brought into best focus by each setting. The second camera should be positioned about 27 centimeters from L, which if possible should have its shutter continually open during the measurement process. The second camera can be digitally (but not optically) zoomed (unless its optical zoom has also been pre-calibrated) to enlarge the image of L during measurement. Once the measurements are available the coefficients of L's focal plane transformation function can easily be calculated from them.

The measurements described above can be repeated for various focus settings of the lens L, giving a focal plane transformation function for each, and the focal plane transformation function for other focus settings of l obtained from these by interpolation. If L has a separate zoom adjustment, this whole group of measurements needs to be repeated for enough zoom settings for focal plane transformation function applicable to the remaining zoom and focus settings to be obtained by interpolation.

A lens L for which all this information is available (in the form of a programmed 3-vector valued function K(focus_setting) or K(focus_setting,zoom_setting) can be called a calibrated lens. Calibrated commercial lenses, telescopes, and microscopes can be combined, and also combined with external lenses, since their focal plane transformation functions simply compound.

Two-dimensional focus more generally. In the preceding paragraphs we have only consiedered rays in the neighborhood of the central ray of a symmetrical 2- dimensional system. We now extend our differential considerations to rays near an arbitrary ray C' passing through a lens. We parametrize rays r near C' by their distance y from C' and their angle t to C'. As above, if r is at distance y from a segment s of C' of length d at its start, and at angle t, then r is at distance y + d sin(t) at the end of s, and the change of angle at an incidence is governed by Snell's' law. Near its center line the surface of the lens can be approximated by a circle of radius R centered at a point p. If Y is the height of this point of incidence I above the circle center p, i's angle fromthe center is arcsin(Y/R), so the normal to the circle at this point is n_Y = [cos(arcsin(Y/R)),-sin(arcsin(Y/R))]. For lines near C' It follows in the same way that

Focus in three dimensions. The phenomenon of focus as described above is inherently two dimensional; in three dimensions we cannot expect the rays emanating from an initial point p at various angles and passing through a lens to come to a common focus unless the lense has some relevant symmetry. In 3 dimensions, the rays c near a central line C are aprartriszed by two distances y,y' and two angles t,t', which for example can be horizontal and vertical distances from the corresponding projections of C, and horizontal and vertical angles from this same projection. After passage through a lens and our usual small-distance approximation, r becomes

The thin lens approximation; adjusted inter-lens distances. The thin lens approximation to the transformation formulas derived above takes d = 0, which reduces the transformation of rays caused by passage through a a single biconvex lens of curvature radii R_1 and R_2 to the product if the matrices

|1            0|   and   |1          	   0|, i.e to |1                       0|
|(c - 1)/R_1  c|         |(1 - 1/c)/R_2  1/c|         |(1 - 1/c)(1/R_1 + 1/R_2)  1|

which we can write as

|1  0|
|a  1|

where a is negative since c < 1 (e.g 2/3). In this drastically simplified approximation, an incoming beam of rays all parallel to the central ray C, which have the form [y,0], are transformed to (y,ay), and so converge to a focus at distance f = -1/a beyond the lens. Rays originating at various angles from a point on the central ray C at distance d in front of the lens have coordinates [dt,t] at incidence to the lens, and so on passage through the lens are transformed to [dt,(1 - d/f)t]. If d/f > 1 these rays come to focus at distance d' = -d/(1 - d/f) beyond the lens. Plainly

1/d + 1/d' = 1/d - (1 - d/f)/d = 1/f.

This is the first 'lens formula' for thin lenses.

If d/f < 1, i. the origin if the rays considered is less than 1 focal length from the lens, then the transformed rays have the form [(d/(1 - d/f))/t,t] on exit from the lens, and so appear to be coming from a point at distance d' = (d/(1 - d/f)) behind the lens. As explained earlier, this defines the position of a virtural plane of focus on which a virtual image is formed. calculating jut as above we have

1/d - 1/d' = 1/f,

which is the variant of the lens formula for virtual images. It is the same as the original lens formula, except that the position of a virtual image must count as negative.

Next consider the family of rays originating at various angles from a point at distance d behind a thin lens and at distance y above the center line. These have the form [y + dt,t] on entry to the lens, and transform into [-y/f + dt ,(1 - d/f)t] and so when they come to focus at a distance -d/(1 - d/f) beyond the lens have the form [y(1 - ad(1 + ad)),(1 + ad)t] = [y(1 - d/f),(1 - d/f)t]. So if d/f > 1, distances y in the source image perpendicular to the center line C are transformed into distances y(1 - d/f) in the refocused image, That is, the source image is inverted and rescaled by the factor (d/f - 1) in the refocused image. Since d' = d/(d/f - 1), the magnification factor m can be written as

m = d/d'.

This is the 'second lens formula', also known as the 'magnification formula'.

If d/f < 1 so that the focus is virtual, much the same calculations apply and formulae result. As before, consider the family of rays originating at various angles from a point at distance d behind a thin lens and at distance y above the center line. So when the these rays come to focus at a distance d/(1 - d/f) before the lens they have the form [y(1 - ad(1 + ad)),(1 + ad)t] = [y(1 - d/f),(1 - d/f)t].

Next we need to consider half-concave and doubly concave lenses in the thin-lens approximation.

These 'lens formulae' are ubiquitous in all elementary textbook and and Web expositions of the ray theory of lenses, though unfortunately the fragmentary discussions generally given do not make their limitations sufficiently clear.

More about the thin-lens approximation. We can reduce the size of the term omitted in the thin-lens approximation in by rewriting the two final matrix terms in the more exact transformation formula,which are

|1 d| * |1          	   0|
|0 1|   |(1 - 1/c)/R_2   1/c|

We rewrite them as

|1          	   0| * |1 d'| + O
|(1 - 1/c)/R_2   1/c|   |0 1 |,    

selecting d' and and then omitting the matrix term term O. Once this has been done the distance transformation matrix

|1 d'|
|0  1|

can be absorbed into the following distance transformation just by adding the distance d' to the inter-lens distance which follows.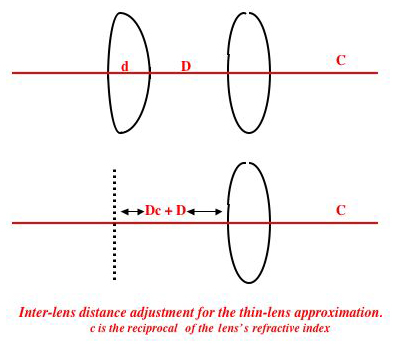

Putting x = (1 - 1/c)/R_2, the first of the above products is

|1         d| and the second is |1 + xdc   d'/c|
|x  xd + 1/c|                   |x         1/c|,

so if we take d' = dc the omitted term is just

|c(1 - 1/c)d/R_2   0|
|0   -(1 - 1/c)d/R_2|.

The advantage here is that for glass c(1 - 1/c) is typically near -2/3*1/2 = 11/3, and that d/R_2, the ratio of the lens thickness to the radius of curvature of its second surface, also tends to be small, e.g. 1/3. So the omitted terms should often be near 1/9 = 0.11 and 1/6 = 0.17, i.e. the omission reduces

|1.11          	          0| to |1          	   0|
|(1 - 1/c)/R_2   1/c - 0.17|    |(1 - 1/c)/R_2   1/c|.

The lens transformation formulae for multi-lens systems work out more favorably if we factor

|1 d| * |1          	   0|
|0 1|   |(1 - 1/c)/R_2   1/c|

|1          	   0| * |1 d'| * |u 0|
|(1 - 1/c)/R_2   1/c|   |0 1 |   |0 v|   ,    

|1                                   d| =  |u 0| * |1 + xdc   d'c| = |u(1 + xdc)   ud'c|
|(1 - 1/c)/R_2  ((1 - 1/c)/R_2)d + 1/c|    |0 v| * |x         1/c| = |vx            v/c|,

so we can take u = 1/(1 + xdc), v = ((c - 1)/R_2)d + 1, ud'c = d, and x = (1 - 1/c)/(vR_2). This expresses

|1 d| * |1          	   0|
|0 1|   |(1 - 1/c)/R_2   1/c|

|1            0| * |1 d| * |1          	   0|
|(c - 1)/R_1  c|   |0 1|   |(1 - 1/c)/R_2   1/c|

then takes on the form

|1             0| * |1                0| * |1 d'| * |u 0|
|(c - 1)/R_1   c|   |(1 - 1/c)/R_2  1/c|   |0 1 |   |0 v|

and so is the product of a thin-lens transformation matrix, a distance transformation matrix, and a diagonal matrix: T₀D₀d₀. Note however that products d₀T₁ of a diagonal matrix and a thin-lens transformation matrix can be written in the form T₂d₀, where T₂ is also a thin-lens transformation matrix. This is because if d₀ and T₁ are

|u 0|     and      |1 0|.
|0 v|              |a 1| 

respectively, then d₀T₁d₀^{- 1} is

|1    0|
|ua/v 1| 

A similar remark applies to products d₀D₁ of a diagonal matrix and a distance transformation matrix. Also, the product of any two diagonal matrices is diagonal. Thus in any extended product of terms T₀D₀d₀, the diagonal matrices can be moved to the left and combined with each other, until the whole product becomes a product of factors T_jD_j, with a final diagonal matrix d_n, amounting to a change of scale for lengths and angles, at the very end. That is, in the first-order two dimensional theory, the working of any system of lenses is exactly that of a flat-lens system, with suitably adjusted radii of curvature and inter-lens distances, followed by a final change of scale for lengths and angles. This expression can be considered to be a canonical form for systems of lenses in the first-order theory.

Working from focal plane positions/magnifications to lens positions/properties. In the thin lens approximation, the action of each 'lens section', i.e. lens and the distance D separating it from the next lens, is described simply by the matrix product

|1 0| * |1 D|
|a 1|   |0 1|

i.e. by two parameters, which determine the focal plane position and a magnification factor according to the formulae given above. It will often be convenient in starting the design of a lens system to specify the focal plane positions and magnifications instead of the lens positions and focal lengths. This alternative specification als give us two parameter, E (inter-focal plane position) and M (plane-to-plane magnification), from which the parameters a and D can readily be calculated. Since each image is the 'object' for the next lens in the sequence, it is enough to give the for the first object-lens-image section of the system. Starting with a family of rays [y,t] at a point on the object, the first lens tranforms them into [y + Dt,a(y + Dt) + t] = [y + Dt,ay + (aD + 1)t], so (as seen above) focus comes at distance D/(aD + 1) behind the lens, at the point [y - ayD/(aD + 1),ay + (aD + 1)t]. So, since the plane of the object is the intial focal plane, we have E = D + D/(aD + 1) for the inter-focal-plane distance and M = 1 - aD/(aD + 1) for the magnification, which is to say that aD = (1 - M)/2, so D = (3/2 - M/2)E/(5/2 - M/2) and a = (1 - M)/(2D).

Suppose, for example, that we want to design a simple two-lens microscope sustem of the kind described in more detail below. This can have an 8" tube, a first real image focused 1 inch from the viewer end of the tube with a 50 times magnification, and , and a second (virtual) image (formed by the microscope eyepiece) at the bottom of the tube with a 90 times magnification, so that seen by an eye positioned exactly at the eyepiece the apparent magnification will be 90/9 = 10, for an overall system magnification of 500.

Optimization of lens properties by 'lens bending' and 'lens subdivision'. In the thin-lens approximation considered above, a lens's focal lenth, and hence its optical activity, depends ony on the sum (1/R_1 + 1/R_2) formed from the radii of curvature of the lens's two surfaces. So variation of R_1 and 1/R_2 in such a way as to keep R_1 + 1/R_2 constant, which is called 'lens bending', would seem to have no effect. However this operation can change, and indeed improve, a lens's higher order properties, e.g. its spherical aberration.

The tilted lens. Next we consider nearly horizontal rays incident on a lens positioned along a central ray C as above, but tilted to the vertical at an angle T. This is the same as considering rays incident at an angle of approximately T on a vertically positioned lens.

Analyzing the working of systems of lenses: the magnifying glass.The preceding formulae, including thin lens approximation and the simplified lens formulas deriving from it, give a good starting point for analyzing the working of systems of lenses. As an example of this, we can consider the simplest lens system of all: a single double-convex lens, used as a 'magnifying glass'. This device has been known for thousands of years, as witness the fact that Aristophanes mentions the burning-lens in his play The Clouds (424 BC). Nevertheless it is not so easy to account fully for the behavior of this instrument, since working with it involves an interplay of its objective optical properties with the properties of the human eye. We begin with the latter issue, since it is the more complicated. As with all instruments which produce a virtual image to be viewed by the eye rather than being projected an a screen, the effect of the eye's lens, and in particular the lens-to-retina relationship, needs to be taken into account. When an image (be it real or virtual) is viewed, the curvature of the eye's lens is automatically and unconsciously adjusted to keep the image in focus. One can see real and virtual images in good focus if they are before one, but not if they are behind. If behind one they are blurry and cannot be brought into focus by the eye (but they are easily brought into focus by either a concave or a convex external lens which moves the focal plane to a position before one). This fact requires explanation, since one does see them in any case, but they are always blurred.

The reason (and here we follow 'Ophthalmology: A Short Textbook' by Gerhard K. Lang, Josef Amann, John Grossman, available as a Google Books Result) lies in the anatomy of the eye's lens and the way in which it adapts its curvature to refocus. The lens is connected by numerous thin fibers (constituting the 'zonule of Zinn') to a ring-shaped muscle (the 'Ciliary muscle'). When under tension the fibers pull on the lens, flattening it and so increasing its focal length. When not under tension, this pull disappears and the lens reverts to its natural most rounded shape, having shortest focal length. Curiously, the Ciliary muscle works on these fibers in reverse fashion: when the muscle contracts the fibers relax, and when it relaxes they come under tension. But once the Ciliary muscle has contracted enough to relieve all the tension in the fibers of the zonule of Zinn, additional contraction will have no effect, since these fibers will only work if pulled, not pushed. So the lens can never get rounder than the shape it assumes when the fibers are relaxed, which means its focal length can grow no shorter. Therefore the eye can focus families of rays diverging from a source in front of it, but not families of rays converging to a destination behind it. For the same reason it can never focus real or virtual images in front of it if they are too close, since this would require a shorter focal length than the shortest of which it is capable. This is the phenomenon of 'near point'. The nominal value of this length is roughly 10 inches, though in supple youngsters it may be much less, and in stiff elders can be more. At any rate there is a whole range of image positions, starting with the eye's near point and extending to all positions behind the head, for which images can never be brought into focus.

Careful observation of the behavior of a magnifying glass shows the following phenomena. If in contact with the object to be magnified it has little effect. When gradually lifted off the object, it magnifies more and more strongly until a certain point, at which the image starts to become blurry. Beyond this distance from the object, the image remains blurry, and at a certain point starts to be not only blurry, but smaller and smaller. These are the phenomena which any careful account of a magnifying glass's behavior must explain.

A typical value for the focal length of a magnifying glass is 10". A five-inch diameter glass of this strength will be about 1/2" thick. So if closer to the object than 10" the glass forms a virtual image, whose distance from the eye must be greater than the viewer's near-point limit if it is not to be seen as blurry; otherwise a real image. If the glass is held somewhere between 11" and 18" from the eye so as to form a real image, and the object at 24", which are about as large as can be comfortable for items hand-held, then the real image formed will be at distance 1/(1/10 -1/13) in front of the lens by the thin-lens formulas given above, which is about 43 inches in front of the lens, and so behind one's head. Even if the object is held 36" from the eye of a long-armed person, the real image formed will be at distance 1/(1/10 -1/25) or 16" in front of the lens, and so still behind one's head. This explains why the real images formed by magnifying glasses are entirely unfamiliar; they cannot be seen in focus. To see them you must have another person hold the magnifier while you back off and view it from several feet behind that person. Doing this you will see the focused real image inside the boundary of the magnifying glass and filling it.

If, as is more customary, the lens is held at a distance less than its focal length from the eye, then if forms a virtual image. For example, if held 9" from the eye, the virtual image will be 1/(1/10 -1/9), or 90" in front of the lens. It will have been magnified by a factor of 10 = 90"/9". However since by our assumption the object is 24" from the lens and the image 90", the effective magnification is 10 * (24/90) = 2.6 (If an object is magnified to the size of Jupiter, but then its image is placed as far way as Jupiter, it will appear no larger.)

This number can be called the 'best focused magnification' obtainable from a magnifying glass.

The fact that a magnified object become blurry when the lens is held too far from it, initially because the virtual image formed has crossed the near-point barrier, and then because it starts to form a real image behind on's head, is sufficiently explained by the account of lens behavior given above.

Let the focal length of this lens be f. Then if it is held a distance d less than f from the object being viewed, a virtual image is formed; if farther away, a real image.

Microscopes, telescopes, and projectors. In its simplest common form, a microscope consists of two optical sections, an 'objective section' (that closest to the object being viewed) and an eyepiece section (that closest to the observer). Each of these can consist of as little as one lens. These two elements are housed within a common tube. The objective section generates a magnified real image, called the 'intermediate image' of the object being viewed. This intermediate image is normally placed rather near the the eyepiece. The eyepiece converts the intermediate image to a still more magnified virtual image, which is typically placed near the bottom of the tube, close to the first delement of the objective section (e.g. the objective lens). So, for example, to have a 10x magnified virtual image (compared to the intermediate image), the intermediate image must be positioned The final magnification achieved is the product of these two magnifications, which often have roughly comparable values.

Here is a quantitative example of what the design of a 100 power microscope with a 7 inch tube could be like. We assume that 1/10 of the magnifying power is provided by the eyepiece, and the rest by the objective.

Telescopes. Telescopes are quite similar to microscopes, in that they also consist of two optical sections, an 'objective section' closest to the object being viewed and an eyepiece section closest to the observer. As with microscopes, each of these can consist of as little as one lens.

Projectors. Projectors are a bit more complex than microscopes, since intense illumination of the slide or other object being viewed is important. A crucial issue in projector design is the choice of source object type to be projected.

Overhead projectors are similar to other projectors, but are designed to use transparencies as objects to be projected, and to throw an image at right angles to the vertical direction of the projector.

Rules for locating focal planes. To understand the action of a series of lenses, a good first step is to find its incoming and outgoing focal lengths. This is easiest if all the lenses are convex and symmetric, and the outgoing focus of each lens lies between it and the next lens in the series. Let the focal length of the j-th lens be f_j and its distance from the next lens be d_j. Then, assuming that the initial lens receives a family of rays parallel to the central ray C, the second lens will see an image positioned at f_1, which it will bring to focus at a distance d_2' ahead of it determined by the equation 1/(d_1 - f_1) + 1/(d_2') = 1/f_2. This consideration repeats for successive lenses, so that we have 1/(d_2 - d_2') + 1/(d_3') = 1/f_3, and in general 1/(d_j - dj_') + 1/(d_(j + 1)') = 1/f_(j + 1), with d_2' = f_1. The final focus lies at a distance d_n' ahead of the n-th and last lens of the series, so the outgoing focal length of the overall series is d_n'.

To extend this discussion to the case in which the point of focus of one lens lies beyond the position of the next lens in sequence, we need to examine the action of a lens surface on a group of rays converging to a point which lies a distance D forward of it along the central ray C. These have the form [y - Dt,t], and so (in the thin-lens approximation) are transformed into [y - Dt,a(y - Dt) + t] = [y - Dt,ay + (1 - aD)t]. These come to focus at the position D/(1 - aD) forward of the lens L. So if L is the last lens in a series, and its distance form the next-to-lis lens is

Next we must consider the case in which one of the lenses in our sequence has a one or two concave surfaces. If there is just one such surface,

Symmetries. In any lens system of the kind we have been considering, there is always one symmetry that can be relied on.

C. Magnification. The magnification of a lens system is the ratio of its source image size to the size of the image, be it real or virtual, on the final focus plane. This satisfies composition rules much like those presented above for the calculation of focal plane position. To understand the situation we must consider a series of cases much like those considered above. fist consider the case all the lenses are convex and symmetric, and the outgoing focus of each lens lies between it and the next lens in the series. Since we know that all the rays emitted from a point converge on the destination focal plane, it is enough to consider rays emanating form various points of a source image in a direction parallel to the central ray C. These have the form (y,0) initially, so after transformation they are (ay,a'y). Assuming that a and a' have opposite signs, these come to focus a distance -

Collimated beams. A group of rays is said to be collimated if they cone from an initial focal point q that has been placed at infinity along the central ray C, or if they will converge a a final focal point at infinity. That is, the rays in a collimated beam are parallel to C. A group of lenses that takes rays with some other focus and turns them into a collimated beam is called a collimator.

D. Intensity. To understand light intensity we can thin of each beam in a set of rays as carrying some fixed amount of energy, which remains unchanged unless the ray encounters an opaque object or passes through some absorbing medium. Thus the intensity of a set of rays within a volume of space is determined by the spacing of a random sampling of the rays in it.

Polarization. Plane, elliptically, and circularly polarized light.

E. Prismatic lenses Refraction at a flat surface separating two zones of different refractive index always forms a focused (often virtual) image of an object. To see this, suppose without loss of generality that the plane P in question is the yz plane, that the source p of the rays lies at distance d in the x direction from P, and that a ray r in which we are interested lies in the xy plane. 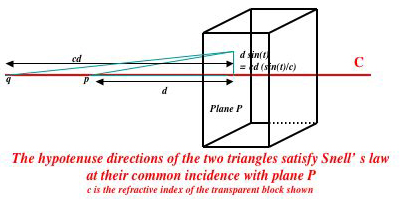Enlarge the smaller triangle seen in the figure, whose hypotenuse is the segment of r between its origin and its intersection with P, by multiplying its base by the factor c, which is the ratio of refractive indices of the exterior and interior media in the figure. Then the hypotenuses of these two triangles satisfy Snell's law at their common point of incidence to the plane P. Hence the vertex q of the larger triangle is the point of (virtual) focus for the point p. This is true for all points lying left of the plane P, so the virtual image formed by P of any object lying left of P is obtained simply by multiplying the distance of each of its points from P by the factor c. Of course, these considerations ignore the variation of refractive index with color, which was the reason that Newton originally interested himself in prisms.

This is all that need be said if we were viewing an object from inside the block shown in the figure. But if we view an object opposite one face of a prism through another face F' of the same prism, the incidence transformation of at exit from F' must also be taken into account. This has the same geometry as the configuration we have just discussed, except that in this case the light rays are leaving an optically denser material for one that is less dense, so the virtual image formed moves nearer to the exit source by the factor 1/c rather than farther from it by the factor c, as discussed above. Thus the virtual image formed by a prism can be calculated in two easy steps.

Note that the virtual image formed by passage of rays through two sides of a prism differs from that formed by passage though just one side, as iv viewing a pencil partially submerged in water, or specks/bubbles inside a glass prism. In this simpler case only one flat-surface incidence transformation is needed. In this case the virtual image seen depends on the face through which it is viewed. Viewed through the top water surface, the pencil appears bent. But if its viewed from the side, the virtual image will have been moved closer to this side, so the object will appear to be slightly larger, with a discontinuity at the water surface.

If a straight object is placed behind a cylindrical lens (e.g. a glass of water), a curiously positioned and shaped virtual image of it is formed. This situation will be analyzed in more detail later.

If an object is viewed through a multifaceted prism of n faces, there can be n/2 faces from which the object is visible and n/2 on the observer side. Thus as many as n²/4 virtual image fragments can be formed. It is this fact that gives cut diamonds their sparkling appearance.

Next we discuss the optical behavior of systems formed by placing one or two plano-convex or plano-concave lenses in immediate contact with one or two of a prism's faces. If convex, the lens at the entering face will, depending on its focal length and the object position, form either a virtual image outside the prism, a real image inside the prism, or a real image beyond the prism. The object image may divide between these two last possibilities.

F. Lenses and mirrors. Optical systems involving lenses and mirrors can be treated in much the same way as above. The transformation of angle at a mirror is simply t to PI - t, which replaces Snell's law for lenses.

G. Diffraction gratings. A diffraction grating consists of a regular pattern of parallel lines. These patterns can be inscribed or transferred in various ways to glass, plastic, or other flat surfaces, or as an array of circles to the convex or concave surface of a lens, etc. The lines in the diffraction pattern are typically evenly spaced by need not be so. For example, the spacing of the lines in such a grating can increase linearly, creating a 'diffraction gradient'.

According to the simplified wave theory of light, a plane of light of wave length lambda falling on a diffraction grating at angle t and passing through it will reappear most strongly at those angles t' for which all the refracted

For gratings of separation less than half the wavelength of the incoming light

So in two dimensions a the incidence effect of a very fine diffraction grating on an incoming ray of light is to reflect it in the line

Lenticular and Integral lens arrays.

A lenticular lens is an array of cylindrical lenses, designed so that when viewed from slightly different angles, different images placed in micro-strips behind each cylinder are brought into focus. Light-minded uses of such lenses include simple animations, morphs, and changes of visible image as one walks by a lenticular lens on whose back several images have been printed in micro-strips. A more technical use is to allow glasses-free stereo viewing of a pair of images. Integral lens arrays resemble lenticular arrays, but make use of a two-dimensional array of many spherical lenselets rather than a 1-dimensional array of cylindrical elements. Both of these array types have been known for many rears, but the additional technical difficulties involved in forming 2D arrays have hampered commercialization of integral arrays. Lenticular arrays are readily available commercially for under $1 per square foot; integral arrays remain specialty laboratory items not available commercially.

Fresnel lenses, prisms, and mirrors.

Fresnel lenses and other 'Fresnelized' optical elements. A Fresnel lens is a lens that has been divided into (typically circular) sections, each of which has then been thinned by removing most of the material between its front a back surfaces. This introduces artifacts into the image, but reduces and flattens the lens very greatly. This 'Fresnel Flattening' can be used for other optical elements such as prisms and mirrors, A Fresnel mirror with two slopes can be used as a beam splitter.

Binocular effects of short focal length Fresnel lenses. A Fresnel (or ordinary) lens of short focal length, e.g. 30mm, will, if held 30mm from an object, form a real image at distance 30mm from the lens. This can be seen within the boundary of the lens as an inverted version of the object. As the lens moves back from this distance the real image moves away from the lens, diminishing in magnification. When this image gets close enough to one's face, the two eyes will see distinctly different images, which will combine binocularly to give the impression that the real image has 'balooned' out toward the viewer. The same effect can be obtained with any short focus lens, for example a 30x jeweler's loupe with a focal length of 6mm.

Depth perception in real images of composite scenes. When we form a real image of a scene containing multiple objects at depths d₁,...d_n behind a lens if focal length f, the images will focus at distances d₁',...d_n' in front of the lens, where in the thin-lens approximation each d_j is related to the corresponding d_j' by the equation

derived above. Since the ordinary rules of binocular perception then apply to the real image formed wen it is viewed, this implies that the perceived depth of elements of the real image will differ significantly from their true depth. Even though objects further forward, hence closer to the lens, will appear further forward in the real image (since d_j' will increase as d_j decreases), this relationship is not linear. In particular, as d_j approaches the value f at which the image formed passes from real to virtual, d_j' will respond with large changes to small changes in d_j. Not also that the real image is always reversed left-to-right, top-to-bottom. It is this reversal that most clearly distinguishes real images from virtual, since in other respects they appear identical to the eye.

Focus imperfections and their correction.

Spherical aberration. Spherical aberration arises from the fact that in a spherical lens the change of tangent angle relative to height near the top of the lens is larger than that near the center of the lens. The focal planes for the upper and lower edges of the lens lie closer to the lens than the focal planes for rays passing through its center. The best way to correct this is to modify the lens shape so that the angle of the normal vector to the curve varies linearly with the vertical distance from the center of the lens. This is no the case for circles; a lens having such a shape is called a perfect lens. If we write the equation for the lens surface as [y,f(y)], the condition that the lens should be perfect is that the manner in which it transforms rays should not change as one goes from the middle to the edges of the lens, i.e. that the transformation matrix formula

|1 + a'd             d|
|a + a' + aa'd  1 + ad|     

derived earlier should hold over the entire surface of the lens. Assume that the lens is symmetric and the the points on its surface are given by [y,f(y)], where our problem is to find the function f. The unit tangent to the surface of the lens at height y is

[1/sqrt(1 + f'(y)²),f'(y)/sqrt(1 + f'(y)²)],

and so the unit normal is

[-f'(y)/sqrt(1 + f'(y)²),1/sqrt(1 + f'(y)²)].

But even if one needs to work with purely spherical lenses, spherical aberration can be corrected pretty well by introducing a second lens, which should be biconcave.

Chromatic aberration and achromat design. Chromatic aberration arises when the refractive index of a medium is dependent on the color of light passing through it. As noted above, this is a common property of glass: for dense flint it goes from 1.8 (blue) to 1.7 (red), while for borosilicate crown it goes from 1.3 (blue) to 1.1 (red). S a lens and lens system will have different focal lengths depending on the color of the light passing through them. For example, a single symmetrical convex lens of dense flint having a 10 cm radius of curvature and a 1 cm thickness, the transformation matrix is

|1        0| |1 1|  |1       0|   (blue light)  and   |1        0| |1 1|  |1       0|    (red light)
|0.94  0.56| |0 1|  |0.08  1.8|                       |0.94  0.58| |0 1|  |0.07  1.7|

These are 

|1.08  1.8|    (blue light) and  |1.07  1.7| (red light)
|1.06 2.7|                     |1.05 2.58|

so the focal lengths are 1.08/1.06 = 1.0188 and 1.0190 respectively.

This difference in focal length means that if focus is precise for one visible color it will be slightly imprecise for all others, causing the focused image seen to be surrounded by a small rainbow halo of these other colors.

Achromat design. We can construct a compound lens having greatly reduced chromatic aberration by putting two lenses made of different kinds of glass in immediate proximity. The first of these lenses should be double convex and the second double concave. It is easiest to work in the thin-lens approximation. Suppose, for example, that first lens is of flint glass goes from 1.8 (blue) to 1.7 (red), while for borosilicate crown it goes from 1.3 (blue) to 1.1 (red). Let the sum (1/R_1 + 1/R_2) of the reciprocal radii of curvatures for the first lens be r, and the corresponding sum (1/R_1' + 1/R_2') for the second (concave) lens be r'. Then the red-light coefficient a in the thin-lens transformation matrix for the first (convex) lens is (1/1.8)r and the blue-light coefficient is (1/1.7)r. Similarly the red-light coefficient for the second (concave) lens is (1/1.3)r' and the blue-light coefficient is (1/1.1)r'. So for the two-lens combination these coefficients are (1/1.8)r - (1/1.3)r' (blue) and (1/1.7)r - (1/1.1)r' (red). Chromatic aberration will be avoided if these quantities are equal, i.e. (1/1.8 - 1/1.7)r = (1/1.3 - 1/1.1)r', that is 0.0326r = 0.1398r'. i.e. r' = 0.233r. This gives a thin-lens transformation coefficient for the two-lens system of (1/1.8) - 0.233(1/1.3)r = 0.376r, compared to the blue-light value of (1/1.8)r = 0.555r. So chromatic correction by the method we have outline loses about 0.32% of the original lens strength.

The human eye and retina. The human eye consists of a lens deformable by attached muscles and a retina, which is a sensory element composed of neurons. For our purposes we can regard the retina as a plane perpendicular to the lens. When viewing an image the level of contrast in the image falling on the retina is detected and the muscles controlling the lens adjust swiftly and unconsciously to maximize this contrast, i.e to focus the image on the retina. This process of sensation is indifferent to whether the image being viewed is real or virtual, since in both cases the rays falling on the lens of the eye appear to originate in some image plane which emits them at various angles from each of its points. (The true difference between a real and a virtual image is that a sheet of paper or sensor place in the plane of a real, but not of a virtual, image will reflect it or sense its focused energy.)

But problems affecting the eye's ability to acquire sharply focused retinal images often arise. The most common are near- and far-sightedness, in which (perhaps because of lengthening or shortening of the eyeball) the lens muscles are unable to pull the lens to the exact shape needed for retinal focus, so even when they have done their best the plane of focus within the eye remains a bit in front of the retina (nearsightedness) or a bit behind it (farsightedness). The second is astigmatism, in which the lens has become a bit asymmetric, and so forms not one but two partially focused images, determined by its different radii of curvature in two orthogonal planes, as explained above. (Astigmatism can co-exist with nearsightedness or farsightedness, if both these planes lie in front of or behind the retina.) These problems are ordinarily diagnosed psychophysically (rather than by objective measurement of lens shape) by an opthamologist, who uses an eye-chart as the object to view and puts a series of corrective lenses in front of the eye, causing the eye muscles to do their best immediately, and then asks how clear an image is sensed. The corrective glasses prescribed then duplicate these optimal corrective lenses. This prescription needs to be made separately for each eye. To correct nearsightedness a lens which shortens the external focal length of they eye-lens combination is used, and to correct farsightedness a lens which enlarges this focal length.

H. The 3D case. In linear approximation the 3D lens case is much like the 2D case, and many of the same formulas can be used if scalars are rewritten as 2-vectors or 2x2 matrices.

I. General nonlinear considerations for thick lenses. The source-to-focus mapping. In the present section we step momentarily out of the linear theory which has confined us till now, and take up considerations relevant to the entire surface of thick lenses, and so to the design of fish-eye and wide-angle lenses. Suppose to begin with that a lens L brings the rays emanating from every source point p to some exact or even approximate focus q. Then we call the mapping which sends each p into the corresponding q the source-to-focus map stf_L for the lens. This is worth considering since it must share the symmetries of L. In particular, if L is a circular cylinder, then stf_L(p) must also be cylindrically symmetric and so can depend only on the distance of p from L. More generally, if L is bounded by a surface of revolution, stf_L(p) will leave planes through the axis of revolution A unchanged, and so can be analyzed in planar cross-section through A.

Astigmatism; principal axes of astigmatism.

J. The quadratic case.

K. First approximation to wave optics. (Gaussian beams)