Several classes of invariants serve to distinguish inequivalent knots. These include the skein polynomials (cf. [Lickorish 1997, Chapter 15]), 'edge-coloring' invariants derived from mappings of the fundamental group of a knot's complement C into an auxiliary group G (cf. [Livingston 1993, pp. 92,98]), and Thurston's more recently discovered invariants, which derive from the hyperbolic geometry of C (cf. [Adams et al, 1991]). The present paper adds one more invariant, an elementary one of 'edge-coloring' type, to this list. The idea involved is simple. Let K be a knot. Let h be any homomorphism of the fundamental group G of the complement C of K into an auxiliary group G. Take a cylindrical neighborhood of K, and in it a curve K' isotopic to K, not intersecting K, and having linking number 0 with K (in the enveloping space E³.) The homotopy class x of K' is uniquely defined up to an inner automorphism yxy^-1, and therefore h(x) is also unique up to inner automorphism. The invariant we note is simply the equivalence class of h(x).

To fill in the details of this idea and indicate how easily our invariant can be calculated, we will proceed combinatorially rather than geometrically. Hence we regard knots as being defined by regular diagrams, two such diagrams representing the same knot if they can be connected by a sequence of 'Reidemeister moves' (cf. [Livingston 1993]), of which there are three types, namely

(R1) Removal of a superfluous twist: becomes

(R2) Removal of a superfluous crossing: 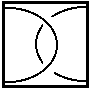becomes

(R3) Harmless passage of an intersection: becomes

For explicit description of a knot's fundamental group and for calculation of the invariant described above, it is convenient to associate the following symbolic descriptor S with regular diagrams of (an oriented) knot. Divide the diagram into arcs each starting and ending at an undercrossing. Start at some convenient edge and assign successive unique names a, b, c,... to the edges. At each undercrossing the undercrossing edge x is terminated by some overcrossing edge y, which approaches x either from the right or from the left. In the first case, append a descriptor xyr to the descriptor S, otherwise append xyl. For example, the descriptor of the trefoil knot is acr,bar,cbr; that of its mirror image is acl,bal,cbl. As this example shows, the descriptor for the mirror image of a knot K is obtained br simply interchanging 'l' and 'r' in K's descriptor.

The standard presentation of a knot's fundamental group is obtained from this descriptor by taking the edge names as generators and writing an equation x' = yxy^-1 (resp. x' = y^-1xy) for each descriptor of the form xyl (resp. xyr), where x' is the edge following x along the knot. (We will call these equations the crossing equations for the given knot diagram. Given a group G, we will call a mapping of the diagram edges into elements of G which satisfies all these equations an allowable marking of the diagram edges by elements of G.) For example, for the trefoil we have the three equations b = c^-1ac, c = a^-1ba, and a = b^-1cb. In these same terms, the invariant to be described in this paper is the (inner automorphism class) of the product

where the (non-commutative group) product shown is formed by traversing the knot edges in x order and writing a factor x^-1y (resp. xy^-1) whenever an edge x is terminated by an overcrossing edge y coming from its right (resp. left). For example, the invariant of the trefoil is a^-1cb^-1ac^-1b, while that of its mirror image is ac^-1ba^-1cb^-1. Note that in formulae of this type, the letters a,b, c etc are taken to be the group elements into which the corresponding edges are mapped by a homomorphism of the fundamental group of the complement C of the knot K into a group G, which is to say a mapping of the edges of K into group elements satisfying all the diagram's crossing equations. (But where it is important to distinguish between an edge x and the group element into which a marking sends it we will write the marking as h(x).) Note that the product we have described will be cyclically rotated depending on the edge of K at which we chose to start, but that all these products belong to the same inner automorphism class since any product and any rotated product derived from it are inner-automorphic.

To show that this product does define an invariant we will show that no Reidemeister move changes its inner automorphism class. For moves (R1), twist removals, this is easy: The only possible marking of a twist is . Hence by our rule removal of a twist just removes a pair a^-1a (or aa^-1) from the product, and so does not change it. For moves (R2), superfluous crossing removals, we argue as follows. The marking of such a crossing must be , possibly with replacement of b by b^-1 if the overcrossing edge must be reversed. Hence by our rule removal of the overcrossing deletes a factor ab^-1(bab^-1)^-1b = aa^-1b^-1b = e from the product, again leaving it unchanged. Finally, for moves (R3), we note that the marking of the crossing before the move must be 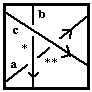, where the edge marked * must carry the marking c^-1bc, and so the edge marked ** must carry the marking (c^-1bc)a(c^-1bc)^-1. Similarly, the marking of the diagram after the move must be . Hence before the move we have a partial product a(c^-1bc)^-1(c^-1bc)a(c^-1bc)^-1c^-1 = aa(c^-1bc)^-1c^-1 = a²c^-1b^-1, while after the move the partial product is ac^-1cac^-1b^-1 = a²c^-1b^-1, which is the same. Therefore this move does not change the overall product. The scrupulous reader will wish to examine the variant cases in which it is either the upper or the lower edge which moves past the intersection of the two others to be assured that these other cases work out in the same way.

This concludes the proof of the invariance we have noted. It is even more elementary to show that in any allowable marking of the edges of a knot diagram all the mark values belong to the same inner automorphism class of the group G, and that the number of markings with values in this automorphism class is an invariant of the (oriented) knot K, independent of the diagram chosen for it; see our preceding citation of [Livingston 1993]. For each such collection of markings we can use the formula (++) to generate a group element which we map into its inner-automorphism class. The collection of all these classes, and hence certainly the number N(K,A) of these classes, which depends only on the knot K and the automorphism class in G which we use to select our allowed markings, is an invariant of G.

The preceding considerations generalize readily from knots to the case of oriented links, in which case a separate invariant of the kind described can be derived for each of the link components, which we can think of as being distinguished by paint of distinct hues. To calculate one of these invariants, we simply traverse one of the components in its given order, and form a product of factors x^-1y (resp. xy^-1) in the manner described above, but only for edges belonging to this component. If, in the argument given above, the edge for which possible changes are considered belongs to the selected component, our arguments apply without change. Since other edges do not enter into the claimed invariant, it is clear that invariance persists.

Note however that caution must be applied in calculating the invariants described above for multi-component links, since they are affected by the orientation of each of the link components, and may also change if the whole configuration is replaced by its mirror image.

Regular diagrams of links can be given descriptors like those used above by defining edges as before, assigning successive edge names in the order of each component and for separate components in any convenient order, and joining the separate component descriptors into a list. For example, the Borromean rings (all oriented counterclockwise) have the descriptor acl,bdr;cel,dfr;eal,fbr.

Computer experiments indicate the potential utility of these invariants. For example, calculating the number of P₇ (permutation group on [1..7]) markings for the trefoil gives the following results. (In each case, the bracketed list shows the cycle structure of the permutations allowed as markings. The integer which follows this list gives the number of markings by permutations having this cycle structure, divided by the total number of permutations with the cycle structure. If any of these markings leads to an invariant, of the kind described above, which is not simply the identity permutation, this is indicated as a count of 'companion classes', written 'cmp.', and we append abbreviated cycle-structure descriptions for these permutation classes.)

	[1, 1, 1, 1, 1, 1, 1]: 1
	[2, 1, 1, 1, 1, 1]: 11
	[2, 2, 1, 1, 1]: 37
	[2, 2, 2, 1]: 15
	[3, 1, 1, 1, 1]: 13
	[3, 2, 1, 1]: 23
	[3, 2, 2]: 1
	[3, 3, 1]: 16
	[4, 1, 1, 1]: 17 [1 cmp.] [2, 2]
	[4, 2, 1]: 19 [1 cmp.] [2, 2]
	[4, 3]: 17 [1 cmp.] [2, 2]
	[5, 1, 1]: 16 [1 cmp.] [5]
	[5, 2]: 16 [1 cmp.] [5]
	[6, 1]: 18
	[7]: 15 [1 cmp.] [7]

	[1, 1, 1, 1, 1, 1, 1]: 1
	[2, 1, 1, 1, 1, 1]: 1
	[2, 2, 1, 1, 1]: 25
	[2, 2, 2, 1]: 25
	[3, 1, 1, 1, 1]: 1
	[3, 2, 1, 1]: 7 [1 cmp.] [3]
	[3, 2, 2]: 37 [1 cmp.] [3]
	[3, 3, 1]: 1
	[4, 1, 1, 1]: 25
	[4, 2, 1]: 9
	[4, 3]: 1
	[5, 1, 1]: 56 [1 cmp.] [5]
	[5, 2]: 16 [1 cmp.] [5]
	[6, 1]: 7 [1 cmp.] [3, 3]
	[7]: 29 [1 cmp.] [7]

	[1, 1, 1, 1, 1, 1, 1]: 1
	[2, 1, 1, 1, 1, 1]: 1
	[2, 2, 1, 1, 1]: 25
	[2, 2, 2, 1]: 25
	[3, 1, 1, 1, 1]: 37 [1 cmp.] [3]
	[3, 2, 1, 1]: 31 [1 cmp.] [3]
	[3, 2, 2]: 1
	[3, 3, 1]: 19 [1 cmp.] [3, 3]
	[4, 1, 1, 1]: 61 [1 cmp.] [2, 2]
	[4, 2, 1]: 77 [1 cmp.] [2, 2]
	[4, 3]: 13 [1 cmp.] [3, 2, 2]
	[5, 1, 1]: 76 [1 cmp.] [5]
	[5, 2]: 6 [1 cmp.] [5]
	[6, 1]: 19 [1 cmp.] [3, 3]
	[7]: 64 [1 cmp.] [7]

The corresponding results for the Borromean rings are

[1, 1, 1, 1, 1, 1, 1]: 1
[2, 1, 1, 1, 1, 1]: 11 [1 cmp.] [3] [1 cmp.] [3] [1 cmp.] [3]
[2, 2, 1, 1, 1]: 37 [2 cmp.] [3, 3] [3] [2 cmp.] [3, 3] [3] [2 cmp.] [3, 3] [3]
[2, 2, 2, 1]: 63 [3 cmp.] [3, 3] [3] [7] [3 cmp.] [3, 3] [3] [7] 
		[3 cmp.] [3, 3] [3] [7]
[3, 1, 1, 1, 1]: 1
[3, 2, 1, 1]: 5 [1 cmp.] [3] [1 cmp.] [3] [1 cmp.] [3]
[3, 2, 2]: 1
[3, 3, 1]: 1
[4, 1, 1, 1]: 17 [2 cmp.] [3, 3] [3] [2 cmp.] [3, 3] [3] [2 cmp.] [3, 3] [3]
[4, 2, 1]: 19 [2 cmp.] [3, 3] [3] [2 cmp.] [3, 3] [3] [2 cmp.] [3, 3] [3]
[4, 3]: 5 [1 cmp.] [3] [1 cmp.] [3] [1 cmp.] [3]
[5, 1, 1]: 1
[5, 2]: 1
[6, 1]: 3 [1 cmp.] [3, 3] [1 cmp.] [3, 3] [1 cmp.] [3, 3]
[7]: 1

Other convenient finite groups are the collection Um(n,p) of unimodular n by n matrices modulo p. In these groups, the collection of all matrices satisfying a specified degree n polynomial equation p(A) = 0 is a union of inner automorphism classes, and, if the roots of this polynomial are distinct, are single automorphism classes.

Bibliography

Adams, C.; Hildebrand, M.; and Weeks, J. (1991) Hyperbolic Invariants of Knots and Links. Trans. Amer. Math. Soc. 326, pp. 1-56, 1991.

Adams, C. (1994) The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman

Murasugi, Kunio (1996) Knot Theory and Its Applications (Bohdan Kurpita, Translator) Springer Verlag

Lickorish, W. B. R (1997) An Introduction to Knot Theory (Graduate Texts in Mathematics, v.175) Springer Verlag

Livingston, Charles (1993) Knot Theory (Carus Mathematical Monographs, No. 24) Mathematical Associationn of America

Thurston,W. P. (1993) Three-Dimensional Geometry and Topology, Princeton University